Was man immer schon über Schärfentiefe wissen wollte...
...und niemals zu fragen wagte
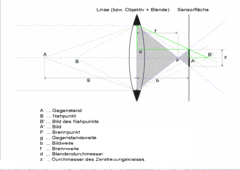
Ein bisschen Geometrie ist schon von Nöten, aber dann kann man schon loslegen und die hyperfokale Distanz verstehen. Nebenstehende Skizze zeigt den geometrischen Sachverhalt (zum Vergrößern draufklicken).
Die beiden grau unterlegten Dreiecke sind ähnlich, und damit ergibt sich sofort f/d = (b-f)/z (Strahlensatz!). f/d ist aber genau die Blendenzahl κ. Also ist b = f + κ⋅z und mit der Linsengleichung (sie lautet: 1/f = 1/g + 1/b) erhält man für die Gegenstandsweite (für b in die Abbildungsgleichung einsetzen!) die Formel
g = f²/κ⋅z + f =: H
Diese Distanz heißt hyperfokale Distanz. Was hat es mit ihr auf sich? Nun, ob das Bild eines Punktes noch als scharf erscheint oder nicht, hängt vom Durchmesser des Flecks, der das Bild dieses Punktes nun einmal ist, ab. Idealerweise wird ein Punkt zwar auf einen Punkt abgebildet, aber das gilt nur für den Fokuspunkt des Objektivs (und da auch nur in guter aber immerhin nur Näherung). Alle anderen Punkte, die vor oder hinter dem Fokuspunkt liegen, werden als Fleck (besser: Scheibchen) am Sensor (bzw. Film) abgebildet. Die Abbildung zeigt ein Scheibchen mit Durchmesser z, dem sogenannten Zerstreuungskreis. Ob unser Auge da noch einen Punkt wahrnimmt oder schon einen Fleck (die empfundene Unschärfe), hängt im wesentlichen vom Bildformat ab und es gilt die Faustregel: ist z kleiner als ein 1500ertsel der gesamten Bilddiagonale, dann erkennt unser Auge noch keine Fleckigkeit des Bildpunktes (äh ... Bildscheibchens).
Die hyperfokale Distanz ist nun die Distanz, auf die das Objektiv fokusiert werden kann (also die Entfernung des Fokuspunktes), bei der Punkte im Unendlichen (also Punkte, die im Brennpunkt scharf abgebildet werden) auf der Bildebene gerade noch scharf erscheinen, also der Bildscheibchendurchmesser noch kleiner als z ist. Diese Situation ist in nebenstehender Skizze dargestellt. Punkte, die nicht näher liegen als der Nahpunkt werden dabei auch noch als scharf abgebildet empfunden.
Der Nahpunkt ist in dem Fall genau bei halber fokaler Distanz: bezeichnet x die Entfernung A'B' und y die Distanz zum Nahpunkt (zu B), dann gilt 1/f = 1/y + 1/(b+x). Der Strahlensatz liefert x/z = (b+x)/d. Daraus x ausdrücken und in die Abbildungsgleichung einsetzen und b noch mit der Beziehung b = f + z⋅κ eliminieren und schließlich y ausdrücken... nach ein bisschen rechnen erhält man dann tatsächlich y = H/2.
Ist das Objektiv derart eingestellt, dass der Fernpunkt (also der Punkt, dessen Bild im Brennpunkt liegt) nicht im Unendlichen liegt, ist der Sachverhalt gleich. Zum Nahpunkt: die beiden grün umrandeten Dreiecke liefern mit dem Strahlensatz x/z = b/(d-z). Die Bildweite des Nahpunktes ist also b+x = b+b⋅z/(d-z). Die Abbildungsgleichung liefert 1/f = 1/(b+b⋅z/(d-z))+1/g' wobei g' eben die gesuchte Etntfernung des Nahpunktes ist. Nach ein bisserl Umformung erhält der Tapfere g' = f⋅d⋅b/(d⋅b-f⋅(d-z)). Da einen b nicht interessiert und im übrigen auch nicht bekannt ist (wenigstens ohne invasive Maßnahmen), aber die Entfernung zum Fokuspunkt schon (die kann man ja leicht steuern, ein Dipper am Auslöser...), nutzt man wieder die Abbildungsgleichung für den Fokuspunkt, um b zu eliminieren. Die liefert b = f⋅g/(g-f). Mit unserem κ=f/d ergibt das wieder nach Rechnerei g' = f²⋅g/(f²-z⋅κ⋅(g-f)). Man ahnt wie es weiter geht: man berechne noch die Distanz zum Fernpunkt, und die Differenz ist dann die Schärfentiefe. Das bleibt dem Leser als Übung überlassen :-)
Unterm Strich, was jeder weiß: wird die Blendenzahl κ kleiner, also die Blendenöffnung größer, dann wird die hyperfokale Entfernung größer, rückt als zum Fernpunkt. Der Nahpunkt rückt dabei natürlich nach und insgesamt nimmt damit die Schärfentiefe ab, die Lichstärke und das Bouquet zu. Gemeinsam mit Abberationen (besser: deren Fehlen) ist das ein wichtiges Qualitätsmerkmal bei Objektiven. Nebenstehendes Bild ist übrigens mit dem Canon EF 85mm 1:1.2 L Objektiv bei κ=1.2 aufgenommen.
Neben den rein geometrisch-optischen Tatsachen spielt aber auch die Wellennatur des Lichts herein, und dabei das Phänomen der Beugung. Ähnlich, wie Wasserwellen sich hinter dem Hafentor annähernd kreisförmig (korrekt: in den geometrischen Schattenraum) fortpflanzen, führt das Phänomen bei optischen Systemen zu Beugungscheibchen, die wieder ab einer bestimmten Größe als Unschärfe empfunden werden (Stichwort Rayleigh-Kriterium). Dabei ist es jetzt umgekehrt: die kleinen Blendenöffnungen erzeugen die Unschärfe, gewöhnlich jenseits von κ=32 beim Kleinbildformat. Allerdings kann es bei hypersensiblen Schmalspurkameras (Xtausend Mp bei kleinem Sensor) schon bei kleineren Blendenzahlen passieren.